▲소수는 약수가 1과 자기 자신밖에 없는 0보다 큰 정수다. (GIB)

소수는 2, 3, 5, 7, 11…처럼 1과 자기 자신으로만 나눠떨어지는 1보다 큰 양의 정수다. 소수는 규칙 없이 드문드문 나온다. 그래서 조금만 더 큰 소수를 찾기만 하면 ‘소수의 규칙’을 발견할 수 있을 것만 같다. 역사 속에서 많은 수학자가 이런 소수의 매력에 빠졌다.

가장 오래된 연구는 고대 그리스의 수학자 유클리드의 ‘원론’에 나온다. 유클리드는 n개의 소수를 선택해 모두 곱한 뒤 1을 더한 수는 소수라고 주장했다. 예를 들어 세 개의 소수 2, 3, 5를 모두 곱한 다음 1을 더한 결과는 소수인 31이다. 유클리드는 이런 원리를 이용해 소수가 무한히 많다고 증명했다.

소수는 대체 어떻게 나타나는 걸까? 1부터 10만 사이의 소수를 1만 단위로 헤아리면, 처음에는 소수가 1229개 등장한다. 하지만 다음에는 1033개, 983개…로 소수의 개수가 점점 줄어든다. 이를 발견한 독일의 수학 천재 카를 프리드리히 가우스는 1부터 숫자 N까지 소수의 개수는 N/(1+1/2+1/3+…+1/N)이라는 식을 만들어냈다.

이 식은 정확하진 않지만 소수의 개수가 대략 몇 개인지는 알려줘 당시 수학계에 큰 파장을 불러 일으켰다. 가우스는 식의 정확성을 높이기 위해 ‘소수 정리’를 만들었다. ‘소수 정리’란 어떤 수 N이 무한히 크다면 1부터 N까지 소수는 N/lnN개라는 것이다. 가우스는 이 정리를 이용해 어떤 큰 수 N이 소수일 확률은 1/lnN이라는 것도 알아냈다. 여기서 ln은 자연로그로, 오일러 수 e를 밑으로 하는 로그함수다.

쌍둥이 소수 추측 : 차이가 2인 소수쌍은 무한할까

대표적인 소수 문제는 ‘쌍둥이 소수 추측’이다. 소수가 무한히 많다는 것을 알았던 고대 그리스 수학자들은 3과 5, 5와 7, 11과 13처럼 그 차이가 2인 소수쌍도 무한히 많다는 ‘쌍둥이 소수 추측’을 떠올렸다. 이 문제는 아직까지 증명되지 않았지만 덕분에 소수와 관련된 연구 성과가 여럿 나왔다.

먼저 소수는 2와 3을 제외하면 모두 6n±1꼴이라는 것이 밝혀졌다. 예를 들어 17은 6의 배수인 18보다 1만큼 작고, 1777은 6의 배수인 1776보다 1만큼 크다. 쌍둥이 소수 쌍도 3과 5를 제외하면 모두 6n±1꼴이 된다. 쌍둥이 소수를 만들어 내는 공식도 고안됐다. 바로 60n2+30n-30±1이다. 하지만 이 식에서는 n이 1에서 13일 때까지만 쌍둥이 소수가 된다.

2013년 4월, 중국의 수학자 이탕 장은 두 수의 차이가 n인 소수쌍이 무한히 많다는 것을 증명했다고 발표했다. 여기서 n은 1부터 7000만까지의 자연수다. 이 증명은 쌍둥이 소수 추측을 해결할 수 있는 실마리를 제공해 수학계를 떠들썩하게 만들었다. 이탕 장의 증명은 소수의 차이가 2, 3, 4, 5, …, 7000만인 소수쌍을 모두 셌을 때 소수쌍이 무한히 많다는 걸 보였다. 이 결과만으론 아직 n이 2일 때의 쌍둥이 소수쌍이 무한히 많은지는 알 수 없다. 하지만 이 차이를 줄이다 보면 언젠가는 쌍둥이 소수가 무한한지 유한한지 알 수 있게 될 것으로 기대된다.

[출처] (GIB)

골드바흐의 추측 : 수를 소수의 합으로 표현할 수 있을까

‘골드바흐의 추측’도 소수에 관한 문제다. 독일의 수학자 크리스티안 골드바흐는 1742년에 ‘2보다 큰 정수는 세 소수의 합으로 표현할 수 있다’는 추측을 적은 편지를 당시 최고의 수학자 레온하르트 오일러에게 보냈다. 오일러는 편지를 꼼꼼히 살펴본 끝에, 그의 추측을 아래와 같이 수정했다.

① 5보다 큰 모든 홀수는 세 소수의 합으로 표현할 수 있다.

② 2보다 큰 짝수는 두 소수의 합으로 표현할 수 있다.

그 이유는 소수에 대한 오일러와 골드바흐의 견해가 달랐기 때문이다. 당시에는 소수의 정의가 확립되지 않아 골드바흐처럼 숫자 1을 소수로 생각하는 수학자가 많았다. 오일러는 숫자 1을 소수로 보지 않았다. 현재 수학자들은 두 번째 명제만을 ‘골드바흐 추측’이라고 부르고, 첫 번째 명제는 ‘약한 골드바흐 추측’이라고 부른다. 그 이유는 2보다 큰 짝수를 두 소수의 합으로 표현한 다음(두 번째 명제 증명), 2보다 큰 소수를 더하면 첫 번째 명제가 되기 때문이다. 하지만 첫 번째 명제를 증명한다고 두 번째 명제가 증명되는 것은 아니다. 홀수를 세 소수의 합으로 표현한 다음 이 중 하나의 소수를 빼면 두 번째 명제가 성립하지 않는 경우가 있기 때문이다.

2013년 5월 페루 수학자 아랄드 엘프고뜨는 약한 골드바흐의 추측을 증명했다고 발표했다. 그는 1030보다 큰 홀수를 세 소수의 합으로 표현할 수 있다고 수학적으로 증명했다. 1030보다 작은 홀수에 대해서는 컴퓨터로 일일이 따져 증명했다. 이탕 장과 아랄드 엘프고뜨의 증명이 맞는지는 현재 관련 분야 유명 수학자들이 꼼꼼히 검토하고 있다.

▲지금도 많은 수학자가 소수 관련 문제에 도전하고 있다. (GIB)

리만가설 : 소수는 역시 악마의 문제인가

소수 연구의 꽃이라면 역시 ‘리만가설’이다. 1859년 독일의 수학자 리만이 제시한 이 가설은 소수로 이루어진 제타함수의 값이 0이 되는 점은 무수히 많고, 이 함수를 복소수 평면 위에 곡면 그래프로 나타내면 함숫값이 0이 되는 점이 모두 일직선(실수 부분이 1/2인 직선) 위에 나타난다는 가설이다. 여기서 제타함수는 모든 양의 정수로 이루어진 식이다.

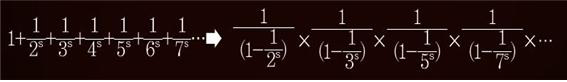
구체적으로, 1부터 차례대로 양의 정수에 역수를 취한 다음, 각각의 수에 S(임의의 복소수) 제곱을 한다. 그리고 모든 수를 더한다. 그런데 이 식에 어떤 수를 곱하고 빼서 변형하면 세상에 존재하는 모든 소수로 이루어진 식으로 바꿀 수 있다. 즉 제타함수는 모든 정수와 모든 소수를 연결하는 불가사의한 식인 셈이다.

그런데 리만가설이 참이라면 제타함수를 그래프로 나타냈을 때 함숫값이 0인 점이 모두 일직선에 나타나게 된다. 이건 불규칙하게 등장하는 소수에도 규칙이 있다는 것을 뜻한다. 이 문제를 풀면 골드바흐의 추측과 같이 소수와 관련된 난제를 단번에 해결할 수 있다. 리만가설에 100만 달러의 현상금이 걸려 있지만 이 가설의 진짜 가치는 무궁무진하다.

리만가설에 도전장을 내민 가장 유명한 수학자가 영화 ‘뷰티풀 마인드’의 주인공 존 내시다. 존 내시는 게임이론으로 노벨경제학상을 받은 천재 수학자다. 내시가 리만가설에 도전한다고 했을 때 수학계는 그가 뛰어난 천재성으로 문제를 증명할 거라고 기대했다. 그러나 1959년 리만가설 발표 100주년 기념 강연 도중 내시는 말을 더듬거리더니, 논리에 맞지 않는 말을 하기 시작했다. 정신분열증이 시작된 것이다. 내시는 30년 뒤에 정신분열증을 치료한 다음 “리만가설의 복잡한 내용에 너무 몰두한 나머지 내 정신이 무너졌다”고 당시를 회상했다.

내시의 강연 직후 리만가설을 연구하던 많은 수학자들은 연구에서 손을 떼기 시작했고, 이런 분위기는 40년 동안 지속됐다. 천재의 정신도 무너뜨리는 무시무시한 연구라는 인식이 생겨버린 것이다. 2000년에 미국 클레이 수학연구소가 리만가설을 7대 수학 난제로 선정하면서 다시 연구에 불이 붙기 시작했다. 이후 많은 수학자들이 도전하고 있지만, 악마의 문제는 아직까지 해결되지 않았다.

▲클레이 연구소가 선정한 7대 문제 중 ‘푸앵카레 추측’을
제외한 6문제가 아직 해결되지 못했다. (GIB)

필자 소개 / 조가현

국내 유일의 수학 잡지 <수학동아>기자다. 최신 수학 연구를 대중에게 쉽게 소개하고, 수학을 주제로 재미와 감동을 주는 글을 쓰기 위해 노력하고 있다.