교집합 [intersection, 交集合]
2016-10-25
2개 이상의 집합에서 모든 집합에 동시에 포함되어 있는 원소로 이루어진 집합을 말하고 공통부분(共通部分)이라고도 한다. A∩B 같이 ‘∩' 기호를 사용하여 교집합을 나타내고 A∩B = { x | x ∈ A 그리고 x ∈ B}임을 의미한다.
예를 들면, 집합 A가 1~10까지의 자연수, 집합 B가 홀수라면 A∩B = {1,3,5,7,9}가 된다. 또 집합 A, B, C의 연산 ∩에 관해서는 아래와 같은 법칙이 성립된다.
① 교환법칙: A∩B = B∩A
② 결합법칙: A∩(B∩C) = (A∩B)∩C
③ 멱등법칙: A∩A = A
④ A⊂B 이면 A∩B = A, A∩Ø = Ø
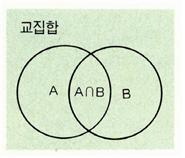
벤다이어그램으로 나타내면 다음과 같다.
- 다음
- 교환법칙 [commutative law, 交換法則] 2016.10.25
- 이전
- 교점정리 [intersection point theorem, 交點定理] 2016.10.25
