KISTI의 과학향기
과학이야기
[과학향기 카드뉴스]겹치지 않는 무한 패턴은 가능할까? 수학계 50년 난제, 비주기적 타일링 해결되다
 2023-08-10
2023-08-10
욕실 타일, 보도블록, 벽지 같은 일상 속 무늬부터
경복궁, 알함브라 궁전 같은 전통 건축물까지
우리는 수많은 반복 패턴을
어렵지 않게 접할 수 있다.
그런데 이런 타일링이
수학계에선 50년도 넘은 어려운 문제다.
일정한 모양이 반복되는 일반 타일링이 아닌,
비슷하면서도 다른 형태로 끝없이 평면을 채우는
비주기적 타일링(aperiodic tiling) 얘기다.
비주기적 타일링을 얻기 위한
학자들의 노력은 1963년부터 가시화됐다.
미국 수학자인 로버트 버거가
도형 2만 426개를 동원해 반복된 형태 없이
평면을 채울 수 있음을 증명한 것이다.
이후 많은 학자들이
비주기적 타일링 문제에 도전했다.
그러다 1974년 수학자 겸 물리학자인
로저 펜로즈가 단 2개의 도형만으로
비주기적 타일링을 구현하는 데 성공했다.
‘도형 하나로 비주기적 타일링 구현하기’는
대표적 수학 난제 중 하나로
많은 이들의 머리를 괴롭혔다.
그런데 최근 50여 년 만에
이에 대한 실마리가 풀렸다.
주인공은 바로,
영국 아마추어 수학자 데이비드 스미스와 그의 연구팀이다.
연구팀은 13각형 도형을 바탕으로 패턴이 겹치지 않는
무한 평면 배치가 가능함을 증명해
학술지 네이처(Nature)에 발표했다.
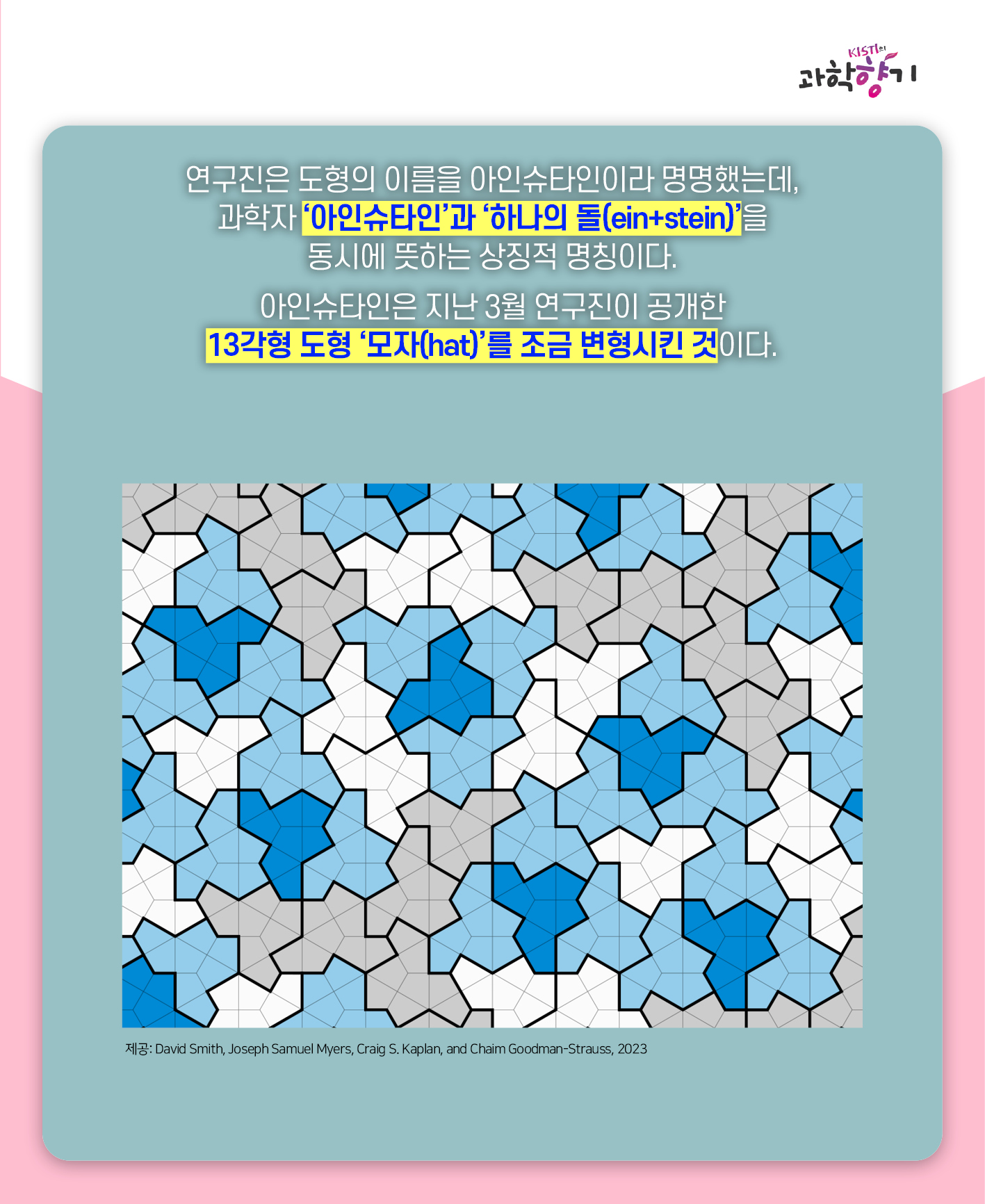
연구진은 도형의 이름을 아인슈타인이라 명명했는데,
과학자 ‘아인슈타인’과 ‘하나의 돌(ein+stein)’을
동시에 뜻하는 상징적 명칭이다.
아인슈타인은 지난 3월 연구진이 공개한
13각형 도형 ‘모자(hat)’를 조금 변형시킨 것이다.
연구진은 출판 전 논문 공유 사이트 아카이브(arXiv)에서
모자를 통해 비주기적 타일링이 가능함을 증명한 바 있다.
모자를 여러 개 연결해 메타타일(metatile)을 만들고,
이를 모아 슈퍼타일(supertile)이 되는 과정을 반복하며
해당 작업이 무한히 계속될 수 있음을 보여준 것이다.
다만 지난 3월 발표에선 ‘모자’와 함께
‘좌우를 바꾼 모자’까지 총 2개 형태가 있어야
이러한 무한 형성이 가능했다.
이에 모자의 모양을 보완해
하나의 형태로도 비주기적 타일링을
구현한 것이다.
도형 하나로 구현 가능한 비주기적 타일링은
수학은 물론 공학에서도 중요도가 높다.
같은 구조 형태가 반복되는 것을 막아
소재의 내구성을 높이는 데 기여할 수 있기 때문이다.
비주기적 타일링과 특히나 연관 깊은
준결정(quasicrystal) 구조는
신소재공학의 중요한 연구 분야 중 하나다.
원자 배열이 규칙적인 결정과
그렇지 않은 비정질의 중간단계로서
마찰력이 적고 강도가 높아
코팅 소재를 만드는 데 유리하기 때문이다.
준결정 구조는
골프채, 면도날, 프라이팬 같은 생활용품부터
엔진 단열재에 이르기까지 그 활용도가 높다.
풀리지 않았던 수학의 신비가 하나씩 밝혀지고
일상 속 소재와도 연관되는 것을 보면
수학이 이론에서 벗어나 현실에서도 무궁무진하게
활용될 수 있다는 것을
다시금 상기하게 된다.
▼ KISTI의 과학향기의 다른 과학 이야기가 궁금하다면? ▼


- 다음
- [과학향기 스토리] 버려진 기저귀로 친환경 콘크리트 집 짓는다?! 2023.08.16
- 이전
- [과학향기 스토리]대변 모으는 은행 있다? 인류를 지킬 데이터 모으기의 세계 2023.08.08

























![[최강기업] 선생님을 위한 기술! 수학 콘텐츠 제작 플랫폼](/jnrepo/upload/cmBbs/202403/ad342aa1323742a7968ed7d6add68f19_1709855725936.jpg)

![[핫클립] 상황의 특수성과 무관한 보편적 원리의 중요성](/jnrepo/uploads/2023/05/hqdefault-11.jpg)

















