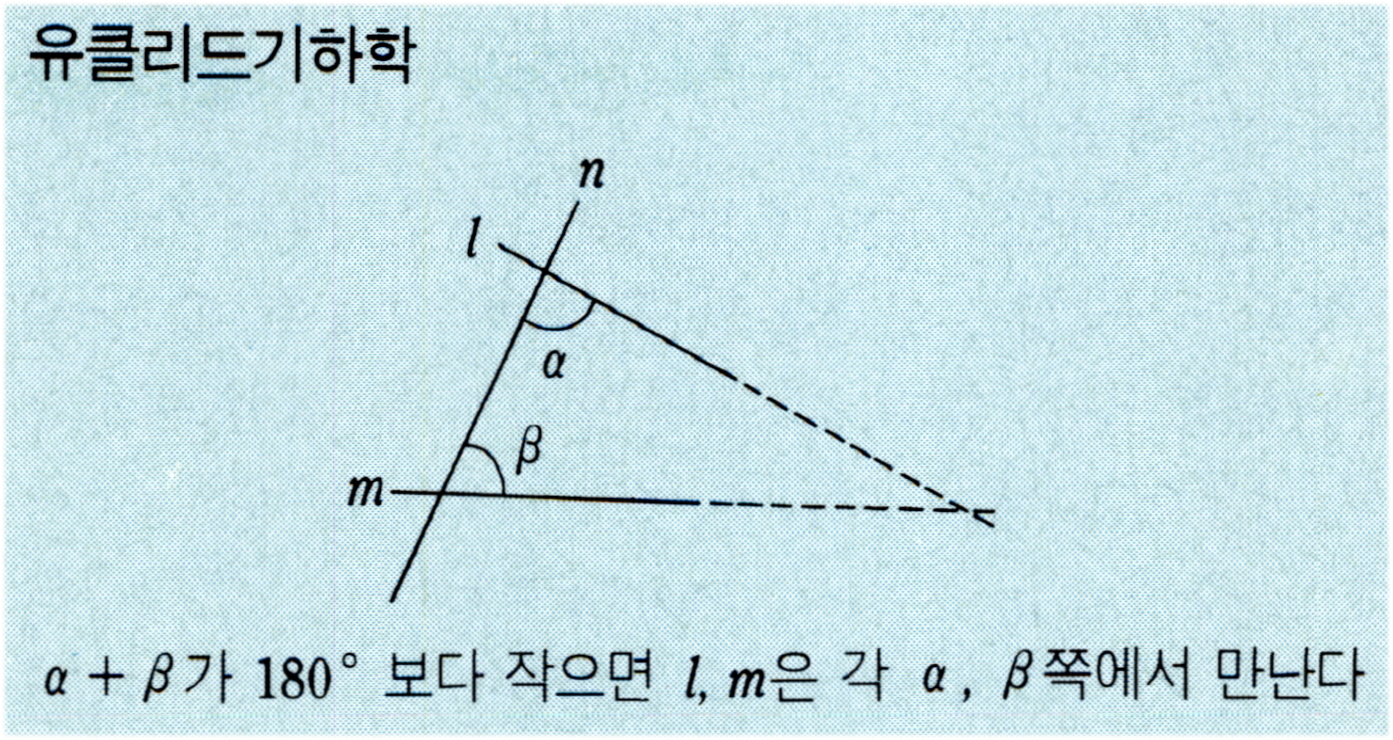
유클리드 기하학(Euclidean geometry)
 2015-09-09
2015-09-09
유클리드 공간에서 성립하는 기하학을 의미한다. 일상적인 공간에서 성립하는 기하학이라고 봐도 무방하다. 유클리드 기하학을 알기 위해서는 유클리드 공간이 아닌 경우가 무엇인지 이해하는 게 중요하다. 예를 들어 우주 공간에서 두 별의 거리를 잰다고 해보자.(상대성 이론 등의 효과는 무시한다.) 이 경우 두 별의 좌표를 알고 있다면 삼차원에서 거리의 공식을 이용해 쉽게 구할 수 있을 것이다. 그런데 서울에서 뉴욕까지의 거리를 구하는 경우를 생각해 보자. 이 경우에도 서울의 좌표와 뉴욕의 좌표를 구해서 거리를 구할 수는 있지만 별 쓸모없는 정보가 될 것이다. 지구 속을 뚫고 지나갈 수는 없기 때문이다. 따라서 표면을 따라 거리를 구해야 하는데, 이때의 최단거리는 유클리드 공간에서의 최단거리(좌표의 차를 이용해 구한 거리)보다 길게 된다. 즉, 지구 표면에서는 유클리드 기하학이 성립하지 않는 비유클리드 공간이라 볼 수 있다. 물론 이러한 일부의 경우를 제외하면 일상생활에서는 대부분 유클리드 기하학으로 해결이 된다.

본 저작물은 공공누리 출처표시+상업적 이용금지 에 따라 이용할 수 있습니다.
- 다음
- 파스칼의 삼각형(Pascal's triangle) 2015.09.09
- 이전
- 간동유적(Ngandong remains) 2015.09.09