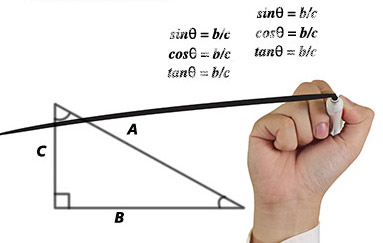
삼각함수와 삼각형의 변과 각 사이의 양적 관계에 입각하여 여러 기하학적 도형을 연구하는 수학의 한 분과. 평면 또는 구면 위 의 삼각형 ABC는 세개의 각 A, B, C와 변 a, b, c의 6요소로 성립되어 있고 삼각함수를 이용하면 이들 6요소 사이의 여러 가지 관계식을 얻을 수 있다.

예를 들면 평면 위의 삼각형에 대해서는

가 성립하고, 구면 위의 삼각형에 대해서는

가 성립한다.

이와 같은 관계식을 기본으로 하고 삼각함수를 응용하여 도형을 연구하는 것이 삼각법이다.

대상이 평면 위의 도형일 때에는 평면삼각법이라 하고, 대상이 구면 위의 도형일 때에는 구면삼각법이라고 한다.

삼각형의 3요소가 주어지고 나머지 3요소를 구하는 것을「삼각형을 푼다」고 하며 이것은 삼각법의 가장 기본적인 문제이다.

삼각법도 원래는 이 문제에서 시작되었고 역사적으로는 천문학상(天文學上)의 응용에서 시작되었기 때문에 구면삼각법이 평면삼각법보다 앞섰다.

고대 이집트·바빌로니아·중국 등에서도 삼각법을 응용했다고 하나 창시자는 B.C. l50년경 그리스의 히파르코스이다.

현재의 삼각법 형식은 독일의 레기오몬타누스(1436~76)에 의한다고 하며 그 모든 정리(定理)는 J. 네이피어, J. 케플러를 거쳐 L. 오일러(1707~83)에 이르러 정비되었다.

삼각법은 천문학·항해술·측지법등에 널리 이용되고 있다.