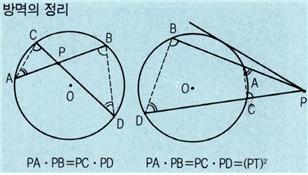
방멱의 정리 (power theorem)
 2017-11-23
2017-11-23
하나의 원과 그 원주 위에 있지 않은 한 점이 있고, 그 점을 지나 원과 만나는 임의의 직선을 그을 때, 직선과 원이 만나는 점과 주어진 점을 연결한 두 선분의 길이의 곱은 항상 일정하다는 정리.
처음에 주어진 한 점을 P라 하고, 점 P를 지나는 직선과 원의 교점을 A, B라 하면 PA · PB는 점 P를 지나는 직선을 어떻게 잡든 일정하며, 그 곱을 점 P에 관한 그 원의 방멱(方冪)이라고 한다. 점 P를 지나는 직선이 원의 접선(接線)이 될 때는 교점 A, B는 일치하여 접점 T가 되고, 방멱은 (PT)2가 된다. 이 정리에서 원에 내접(內接)하는 사각형의 경우 두 개의 대각선에 있어 그 교점(交點)으로 나누어지는 선분의 곱은 같아지게 된다. 그러한 성질은 사각형이 원에 내접하기 위한 하나의 조건이기도 하다. 이들 정리는 원주각(圓周角)에 관한 정리나 삼각형의 닮음조건과 밀접한 관계가 있다.

- 다음
- 방심 (excenter, 傍心) 2017.11.23
- 이전
- 발산 (divergence, 發散) 2017.11.23






























