변수가 0에 수렴할 때 그 변수는 무한소가 된다고 말하고, 무한소가 되는 변수를 약해서 무한소라고 한다. 즉, 함수 f(x)에 대해서 x→a(또는 x→a⁺⁰, x→a^-0 일 때 f(x)→0이 된다고 하면 ‘x→a일 때 f(x)는 무한소라고 한다. 2개의 무한소 f(x), g(x)에 대해 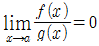이면 f(x)는g(x)보다 고위의 무한소라 하고 이것을 f(x)=O(g(x))로 나타낸다. 또 x=a의 근방에서 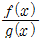가 유계이면 f(x)=O(g(x))로 나타내고 f(x)와 g(x)는 동위의 무한소라고 한다. 특히 f(x)와 gⁿ(x)이 동위의 무한소일 때 f(x)는 g(x)에 대해 n위의 무한소라고 한다. 기약분수식 F(x)/G(x)에 따라서 나타내는 유리함수에 있어서 분모 F(x)가 인수 x-a를 n개 포함한다면 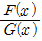는 x=a에 있어서 무한소이고 위수는 x^-a에 대해 n위이다. 또 F, G의 차수를 각각 k, l이라 할 때, k<l 이면 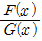는 x = ±∞에 있어서 무한소이고 그 위수는 l/x에 대해 (l-k) 위이다. 무한소의 개념은 다변수의 함수 또는 위상공간의 부분집합에 있어서 정의된 복소수값 함수에 대해서도 적용된다.