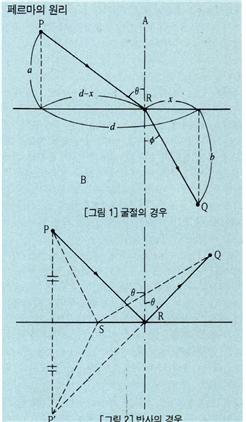
빛의 진행경로에 대한 페르마의 원리는, 1661년에 프랑스의 수학자 페르마(Pierre de Fermat)가 극대극소 문제의 해법을 광학에 접목하여 만들어낸 원리로 최단시간의 원리라고도 한다. 두 점 사이를 진행하는 빛의 경로는 기하학적으로 가능한 경로 중에서 소요시간이 극소(極小)인 경로」라고 표현된다. 이것으로부터 광선의 반사·굴절과, 불균일 매질(媒質)에서의 빛의 경로를 결정할 수 있다. 광속 V_A, V_B인 매질 A, B가 평면에서 접할 때, 빛이 P→R→Q로 진행하는 소요시간 t는 [그림 1]에 의해 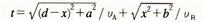이다. t가 극값을 취하는 조건에서는 V_A/ V_B=sinθ/sinφ를 얻으며, 이것은 굴절의 법칙이 된다. 반사의 법칙에 대하여는 [그림 2]에서 실제 경로 P→R→Q가 최단시간이 됨을 알 수 있다. 소요시간 대신에 광학거리(光學距離 ; 진로의 각 부분의 길이에 그 부분의 절대굴절률을 곱한 양의 합)로 표현해도 좋다.