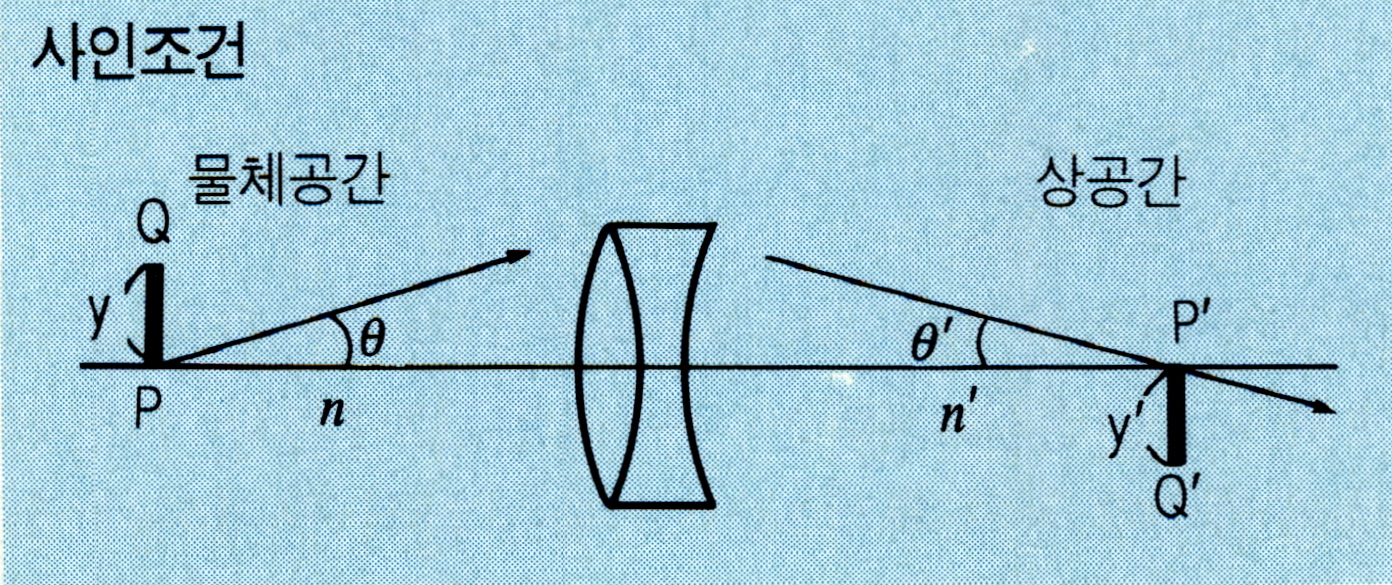
구면수차(球面收差)가 없는 결상계(結像系)에서 광축 위의 물점을 통하는 축과 수직면 내에 있는 물점의 상이 본래의 상점을 지나는 축과 수직면 내에 수차 없이 결상되는 조건. 광학계의 축 위의 물점을 P, P’, 이들 점을 지나 축과 수직면 안에 있는 가까운 두 점을 각기 Q, Q’라고 하면 사인조건은 ny sin θ =n’y’ sin θ ’가 된다. 사인조건은 각 θ의 변화와 상관없이 일정하다. n, n’는 물체공간 및 상공간의 굴절률이다. y, y’는 PQ, P’Q’의 거리이고 θ, θ’는 P에서 나온 광선이 축과 이루는 각 및 그 광선이 굴절한 뒤 P’에서 축과 이루는 각이다. 물점 P가 무한원일 때 입사광선 축의 높이를h, 상공간의 초점거리를f’라 하면 사인조건은 h값에 관계 없이 h/sinθ’=f’가 성립한다. 1879년 독일의 E. 아베가 도입했기 때문에 아베의 사인조건이라고도 한다. 코마수차를 제거하는 조건이 된다.