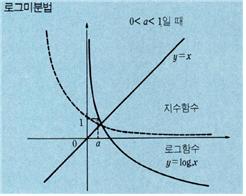
로그미분법(logarithmic differentiation)
 2017-05-04
2017-05-04
주어진 함수 y=f(x)에 대해 y의 로그함수를 z=log y 라고 하면, z는 x의 함수이므로
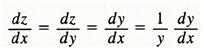 따라서
따라서 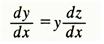 가 된다.
이 사실에서 직접 dy/dx를 계산하기보다 dz/dx를 계산하기 쉬울 때는 dz/dx를 계산해 dy/dx를 구할 수 있다. 이와 같이 로그함수로 고쳐 미분하는 방법을 로그미분법이라 한다.
로그미분법을 쓰면 임의의 실수 a에 대해 y = xa의 도함수는 a가 양의 정수 또는 일반적으로 유리수인 경우의 확장으로서 y’= ax-1 이 됨을 알 수 있다. 즉, log y = a log x 이므로 양변을 x로 미분하면 다음과 같다.
가 된다.
이 사실에서 직접 dy/dx를 계산하기보다 dz/dx를 계산하기 쉬울 때는 dz/dx를 계산해 dy/dx를 구할 수 있다. 이와 같이 로그함수로 고쳐 미분하는 방법을 로그미분법이라 한다.
로그미분법을 쓰면 임의의 실수 a에 대해 y = xa의 도함수는 a가 양의 정수 또는 일반적으로 유리수인 경우의 확장으로서 y’= ax-1 이 됨을 알 수 있다. 즉, log y = a log x 이므로 양변을 x로 미분하면 다음과 같다.
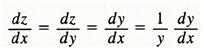 따라서
따라서 - 다음
- 로그방정식(logarithmic equation) 2017.05.04
- 이전
- 로그나선(logarithmic spiral ) 2017.05.04