[요약] 행성이 그 부근의 위성에 미치는 조석작용으로 인해 더 이상 접근하면 위성이 분쇄되어 버리는 행성과 위성간의 최단거리. 행성이 그 부근의 위성에 미치는 조석작용으로 인해 더 이상 접근하면 위성이 분쇄되어 버리는 행성과 위성간의 최단거리. 1850년 E. A. 로시가 그 거리(r)를 이론적으로 연구하여 2.4554(d/d)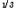R로 계산했다. 여기서 d는 행성의 평균밀도, d는 위성의 밀도, R는 행성의 반지름이다. 이 식을 유도할 때 로시는 위성이 액체상이고, 분자력 같은 조석력 이외의 힘이 없다는 가정 하에 계산했다. 만일 위성이 위 식의 거리보다 행성에 더 가까워지면 위성은 일정한 형태를 유지하지 못하게 되고 결국 작은 유체덩어리로 분산될 것이다. 이 한계거리를 로시한계라고 한다. 위 식의 계수 2.4554는 뒷날 G. H. 다윈이 다시 계산하여 244로 산출했다. 실제로 위성은 고체이기 때문에 액체상 위성보다 분쇄되기 어렵다. 그러나 위성이 암석으로 되었어도 그 형태가 자기중력으로 유지될 정도로 질량이 크면, 유체의 경우와 통일하게 다룰 수 있다.