[요약] 무한수열의 a₁, a₂, a₃, …, a_n, … (a_n≠0)의 각 항을 곱해서 a₁·a₂·a₃·…·a_n·…과 같은 꼴로 만든 식, 무한승적(無限乘積)이라고도 한다. 무한수열의 a₁, a₂, a₃, …, a_n, … (an≠0)의 각 항을 곱해서 a₁·a₂·a₃·…·a_n·…과 같은 꼴로 만든 식, 무한승적(無限乘積)이라고도 하며 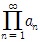 또는 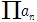 으로 나타낸다. 최초의 n항의 곱 p_n=a₁·a₂·a₃·…·a_n을 제n부분곱이라 하고, 수열 {p_n}이 0이 아닌 극한값 p에 수렴할 때 이 무한곱은 p에 수렴한다고 하며 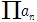=p라고 쓴다. 이 때 p를 이 무한곱의 곱이라고 한다. {p_n}이 수렴하지 않거나 또는 0에 수렴할 때 무한곱은 발산한다고 하지 않는다. 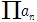이 수렴하면 a_n-1이지만 그 역은 성립하지 않는다. 무한곱은 그 항을 1+a_n(a_n→0)이라 쓰고 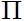(1+a_n)의 형으로 취급하는 것이 편리하다. 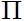(1+a_n)과 ∑log(1+a_n)은 동시에 수렴 또는 발산한다. a_n≥0이라면 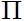(1+a_n)과 ∑a_n은 동시에 수렴 또는 발산한다. 무한곱 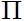(1+∣a_n∣)이 수렴할 때 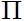(1+a_n)은 절대수렴한다. 절대수렴하는 무한곱의 값은 항의 순서에 관계없다. 무한곱의 공식 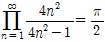,  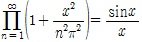등은 유명하다.