[요약] 미지수에 관한 무리식을 포함한 부등식이다. 무리식을 포함하는 부등식으로 실수의 범위 내에서 취급되므로 무리부등식의 해(解)를 구할 때는 근호 내부가 양(+) 또는 0의 조건에 주의해야 한다. 예를 들면 무리부등식 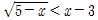을 풀 때는 좌변 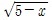가 실수인 조건, 즉 5-x≥0, x≤5를 만족시켜야 한다. 또 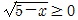이므로 당연히 우변도 x-3>0의 조건, 즉 x>3을 만족시켜야 한다. 곧 x의 범위를 3<x≤5 에서 생각한다. 다음은 3<x≤5의 범위에서 양변은 모두 양(+)또는 0이므로 부등식의 양변을 제곱해도 부등호의 방향은 변하지 않는다. 즉, 5-x<(x-3)²이고 이것을 정리하면 x²-5x+4>0, (x-1)(x-4)>0이므로 x>4, 또는 x<1이 된다. 그런데 3<x≤5의 범위를 만족시켜야 하므로 이 부등식의 해는 4<x≤5가 된다. 이와 같은 무리부등식의 해를 일반적인 꼴로 나타내면 다음과 같다. ① 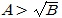의 해는 B≥0, A>0, A²>B인 세 부등식을 모두 만족시키는 x의 범위이다. 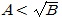② 의 해는 B≥0, A<0의 공통인 범위와 B≥0, A≥0, A²<B의 공통 범위를 합한 것이다. 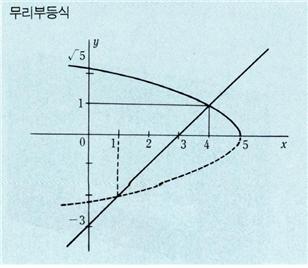이상은 계산에 의한 해법이며, 그래프에 의한 해법도 생각할 수 있다. 위의 식 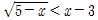을 그래프에 의해 구하려면 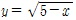와 y=x-3의 그래프를 그려서 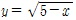의 그래프가 y=x-3의 그래프보다 아래에 있을 x의 범위를 구하면 된다. 여기서 두 그래프의 교점의 x좌표는 무리방정식 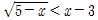의 해인 x=4이므로, 구하는 해는 4<x≤5임을 알 수 있다.