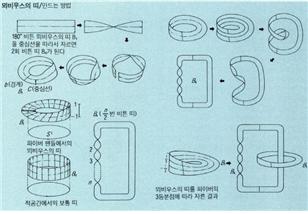
[요약] 좁고 긴 직사각형 종이를 180° 꼬아서 끝을 붙인 면과 동일한 위상기하학적 성질을 가지는 곡면을 말한다. 위상기하학적(位相幾何學的) 성질을 가진 곡면. 좁고 긴 직사각형의 종이를 180˚(한번) 꼬아 양 끝의 두 변을 반대방향으로 붙이면 [그림]의 B₁과 같은 곡면을 얻는다. 이 곡면 위의 한 점에서 선을 그어 종이를 한 바퀴 돌아 본래의 위치에 돌아오면 최초의 면과 반대면이 되므로 이 곡면은 바깥쪽과 안쪽의 구별이 없는 면(단측면〈單側面〉)임을 알 수 있다. 곡면의 이러한 성질을 처음 지적한 A. F. 뫼비우스를 기념하기 위해 이 곡면을 「뫼비우스의 띠」라고 부른다. 보통의 띠 B₀는 직사각형의 좌·우변을 붙이면 얻을 수 있다. 이 B_o와 B₁같은 호몰로지군(homology group)을 가지지만, 동상(同相)은 아니다. 가부호(可符號)성도 경계의 수도 일치하지 않는다. 일반적으로 n을 정수라 하고 180˚×n만큼(n회) 꼬아서 얻어지는 띠를 B_n이라 하면, n=2k일 때 B_n과 B_o는 동상이며, n=2k+1일때 B_n과 B₁은 동상이다. 그러나 동상이라고 해도 공간 속에서 같은 위치에 있는 것은 아니다. 보통의 띠 (B_o)를 중심선에 따라 자르면 2개의 띠로 분리된다. 그러나 뫼비우스의 띠 B₁을 중심선을 따라 자르면 2회 비튼 하나의 띠 B₄가 된다. 또 뫼비우스의 띠를 파이버의 3등분점을 따라서 자르면 1개의 뫼비우스의 띠 B₁과 2회 비튼 B₄띠 가 서로 분리되어 얽혀 있는 상태가 된다.