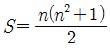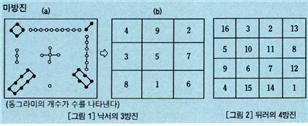
[요약] 1에서 n²까지의 정수를 n행 n열의 정사각형 모양으로 나열하여 가로, 세로, 대각선의 합이 전부 같아지도록 한 것이다. 1에서 n²까지의 양의 정수를 정사각형으로 배열하여 가로, 세로, 대각선상으로 합계가 모두 같도록 만든 것으로 간단히 방진이라고도 한다. 마방진의 각 칸을 셀(cell)이라 하고 각 변에 나열된 셀의 개수에 따라 3방진, 4방진, …, n방진이라 한다. 대부분의 마방진에 쓰이는 정수는 1부터의 연속수이며 가로, 세로, 두 대각선의 각각의 합 로 표시된다. 따라서 3방진은 S=15, 4방진은 S=34, 5방진은 S=65가 된다. 마방진의 역사는 오래되었으며 전설에 의하면 B.C. 2000년경 우(禹)가 낙수(落水)의 치수공사를 하고 있을 때 등에 [그림 1-(a)]와 같은 도형이 그려진 거북이 나타났다고 하며 이 도형이 [그림 1-(b)]와 같은 3방진이다. 이 도형을 낙도(洛圖)·하도(河圖)·낙서(洛書)라 하였고, 중앙의 5는 오행수(五行數)에 대응하여 우주를 상징한다. 마방진은 그 후 한국과 일본·인도 등지로 전파되었고, 15세기에 비잔틴의 작가 E. 모소플루스에 의해 서양에 소개되었다. 마방진이 서양에 알려진 것은 동양보다 늦었으나 만드는 방법은 서양에서 먼저 발견되어, 기록에 나타난 최초의 것은 A. 뒤러의 동판화《멜랑콜리아》(1514)로, 4방진으로 제작된 날짜가 맨 아랫줄 중간에 들어가 있는 것이 특징이다[그림 2]. 16세기에 이르러 독일·프랑스에서 마방전에 대한 연구가 시작되어 1900년을 전후해 미국에서 유행했다. 중국에서는 양휘(楊輝)의 연구가 유명하며, 우리나라에서는 조선 숙종 때 영의정을 지낸 수학자 최석정(崔錫鼎)이 절묘한 마방진을 창안하여 그의 저서《구수략(九數略)》에 실었다. 이 책에 있는 마방진은 1부터 81까지의 정수를 중복 없이 배열한 것이며 큰 사각형 전체로도 마방진(가로·세로로만 합이 같다)이 될 뿐 아니라, 그 안에 있는 9개의 정사각형도 역시 마방진을 이루고 있다.