도플러효과(Doppler effect)
 2017-01-25
2017-01-25
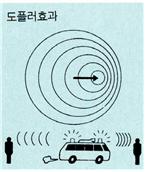
파원(波源)과 관측자 중 한쪽 또는 양쪽 모두가 운동하고 있을 때 관측자에게 관측되는 파원의 진동수가 변하는 현상. 1842년 오스트리아의 물리학자 J. C. 도플러가 이중성(二重性)의 빛에 관하여 별의 운동방향과 색의 변화를 연구하던 중 처음 발견했다.
파동을 방출하는 전파, 광, 음의 주파수가 변화하는 현상. 발생한 위치(발생점)와 관측자의 위치(관측점)가 둘 다 이동하거나 한쪽이 이동할 때 생기는 현상이다.
발생점과 관측점이 가까우면 주파수가 높아지고, 멀어지면 주파수가 낮아지는데 이것은 실제 측정값과 다르게 나타난다. 주파수의 관측값 변화는 파동의 전파속도와 파원에 대한 관측자의 상대속도에 따라 정해진다. 그러나 파동속도에 대하여 파원과 관측자 사이의 상대속도가 아주 작은 경우에는 관측하기 어렵다.
도플러(1542년)가 처음 발견한 것으로 별의 시선속도를 결정하는 기초로 오래 전부터 천문학에서 이용해왔다. E.허블이 이를 바탕으로 성운거리와 후퇴속도의 관계를 발견하여 팽창우주를 증명한다.
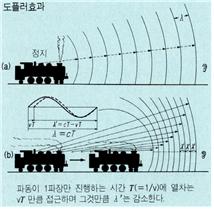
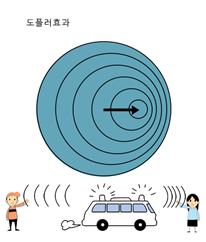 〔음파의 도플러 효과〕 정지해 있는 관측자 쪽으로 진동수
〔음파의 도플러 효과〕 정지해 있는 관측자 쪽으로 진동수 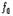 (Hz)의 음을 내는 음원(音源)이 속도
(Hz)의 음을 내는 음원(音源)이 속도 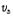 (m/s)로 접근하는 경우를 가정하자. 음의 속도는
(m/s)로 접근하는 경우를 가정하자. 음의 속도는 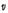 (m/s)라 한다. 어느 순간에 음원에서 나온 음파의 마루는 1초 사이에
(m/s)라 한다. 어느 순간에 음원에서 나온 음파의 마루는 1초 사이에 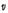 만큼 진행한다. 이 사이에 음원도
만큼 진행한다. 이 사이에 음원도 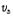 만큼 진행하고 음파의 마루를
만큼 진행하고 음파의 마루를 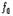 개 낸다. 음원이 진행하는 방향에서는
개 낸다. 음원이 진행하는 방향에서는 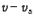 사이에 파의 마루가
사이에 파의 마루가 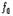 개 있으므로 파장은
개 있으므로 파장은 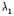 =(
=(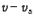 )/
)/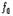 가 되어, 음원이 정지하고 있을 때보다 짧아진다. 그러나 파의 진행속도는 변하지 않기 때문에 관측자에게서는 그 음의 진동수가
가 되어, 음원이 정지하고 있을 때보다 짧아진다. 그러나 파의 진행속도는 변하지 않기 때문에 관측자에게서는 그 음의 진동수가 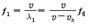 가 된다. 즉, 진동수가 증가되어 실제의 음보다 높은 소리로 들린다. 반대로 음원이 멀어질 경우에는
가 된다. 즉, 진동수가 증가되어 실제의 음보다 높은 소리로 들린다. 반대로 음원이 멀어질 경우에는 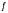 ′1 =
′1 = 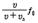 가 된다.
다음에 음원이 정지해 있고 관측자가 음원 쪽으로
가 된다.
다음에 음원이 정지해 있고 관측자가 음원 쪽으로 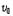 (m/s)의 속도로 접근해 가는 경우를 가정해 보자. 음원이 정지해 있기 때문에 공간을 전파하는 음파의 파장은 변함이 없어
(m/s)의 속도로 접근해 가는 경우를 가정해 보자. 음원이 정지해 있기 때문에 공간을 전파하는 음파의 파장은 변함이 없어 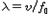 이다. 그러나 운동하고 있는 관측자에 대해 파의 마루는 속도
이다. 그러나 운동하고 있는 관측자에 대해 파의 마루는 속도 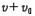 로 다가간다. 그 결과 관측자에게는 파의 진동수는
로 다가간다. 그 결과 관측자에게는 파의 진동수는 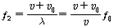 가 된다. 음원 및 관측자가 모두 운동할 때는 음원에서 관측자 쪽으로 가는 방향을 양으로 하여 속도를 각각
가 된다. 음원 및 관측자가 모두 운동할 때는 음원에서 관측자 쪽으로 가는 방향을 양으로 하여 속도를 각각 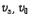 라고 정하면, 그 진동수는
라고 정하면, 그 진동수는 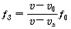 가 된다.
〔광파의 도플러 효과〕도플러 효과는 음파뿐 아니라 모든 파동현상에서 일어난다. 다만 빛의 경우에는 빛의 속도가 매우 빨라 도플러 효과의 영향이 미미하다. 그래서 광원과 관측자의 상대속도가 광속에 비교할 수 있을 정도로 충분히 빠를 때에만 관측된다. 특수상대성이론은 로렌츠 변환을 이용하여 기술한다. 음파와 다른 점은 어느 좌표계(관성계)에서도 진공 속의 광속
가 된다.
〔광파의 도플러 효과〕도플러 효과는 음파뿐 아니라 모든 파동현상에서 일어난다. 다만 빛의 경우에는 빛의 속도가 매우 빨라 도플러 효과의 영향이 미미하다. 그래서 광원과 관측자의 상대속도가 광속에 비교할 수 있을 정도로 충분히 빠를 때에만 관측된다. 특수상대성이론은 로렌츠 변환을 이용하여 기술한다. 음파와 다른 점은 어느 좌표계(관성계)에서도 진공 속의 광속 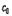 가 일정한 값을 가지는 것이다. 광원의 좌표계가 관측자의 좌표계 쪽으로 속도
가 일정한 값을 가지는 것이다. 광원의 좌표계가 관측자의 좌표계 쪽으로 속도 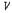 로 병진운동을 할 때, 그 광원이 복사하는 진동수
로 병진운동을 할 때, 그 광원이 복사하는 진동수 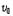 의 광파가
의 광파가 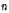 방향으로 진행하고 관측자에게는 진동수
방향으로 진행하고 관측자에게는 진동수 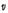 로 관측된다. 이 진동수의 비는
로 관측된다. 이 진동수의 비는 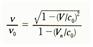 이다. 여기서
이다. 여기서 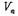 은 속도
은 속도 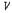 의
의 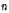 방향 성분이다. 특히
방향 성분이다. 특히 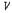 가
가 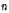 에 평행한 경우는
에 평행한 경우는 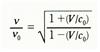 이고,
이고, 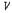 가
가 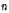 에 반대방향으로 평행하다면
에 반대방향으로 평행하다면 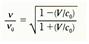 가 된다. 이들의 비는 (
가 된다. 이들의 비는 (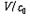 )2 이 1에 비해 무시될 수 있을 때에만 음파의 도플러 효과의 식과 같은 형식이 된다. 즉,
)2 이 1에 비해 무시될 수 있을 때에만 음파의 도플러 효과의 식과 같은 형식이 된다. 즉, 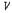 가
가 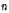 에 수직인 경우를 예로 들면
에 수직인 경우를 예로 들면 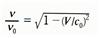 이 된다. 이 진동수의 비는
이 된다. 이 진동수의 비는 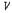 가 크고 (
가 크고 (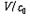 )2 이 1에 비하여 무시될 수 있을 때에만 1과 다른 값을 가진다. 이것은 광파에서만 볼 수 있는 효과로 가로의 도플러 효과라고 한다. 별이나 성운 중에는 지구에 대하여 시선방향으로 매우 큰 상대속도를 갖고 멀어져 가는 것이 있다. 그 스펙트럼을 정밀분석하면 특정원자의 선스펙트럼이 도플러 효과에 의하여 적색이동을 일으킴을 알 수 있다.
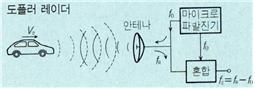
〔마이크로파의 도플러 효과〕항공기나 자동차의 속도측정에 응용된다. 또한 레이저광의 도플러 효과를 이용하여 액체의 유속을 측정하는 도플러 유속계도 실용화되었다.
)2 이 1에 비하여 무시될 수 있을 때에만 1과 다른 값을 가진다. 이것은 광파에서만 볼 수 있는 효과로 가로의 도플러 효과라고 한다. 별이나 성운 중에는 지구에 대하여 시선방향으로 매우 큰 상대속도를 갖고 멀어져 가는 것이 있다. 그 스펙트럼을 정밀분석하면 특정원자의 선스펙트럼이 도플러 효과에 의하여 적색이동을 일으킴을 알 수 있다.
〔마이크로파의 도플러 효과〕항공기나 자동차의 속도측정에 응용된다. 또한 레이저광의 도플러 효과를 이용하여 액체의 유속을 측정하는 도플러 유속계도 실용화되었다.
 〔음파의 도플러 효과〕 정지해 있는 관측자 쪽으로 진동수
〔음파의 도플러 효과〕 정지해 있는 관측자 쪽으로 진동수 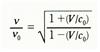 이고,
이고, 


- 다음
- 돋보기(magnifying glass) 2017.01.25
- 이전
- 니콜라 테슬라 [Nikola Tesla, 1856.07.10 ~ 1943.01.07] 2017.01.25













![[핫클립] 전자파를 차단하는 전자파 차폐 신소재](/jnrepo/uploads/2023/10/7-2.jpg)
![[다큐S프라임] 소리로 바다를 보는 수중음향 기술](/jnrepo/uploads/2023/10/111-1.jpg)
![[과학뉴스] 버려지는 몸속 전기 에너지로 치료 효과 높인다](/jnrepo/uploads/2023/07/hqdefault-3-31.jpg)

















