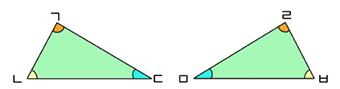
서로 닮은 두 개의 도형에서 대응하는 변, 각, 점을 각각 대응변, 대응각, 대응점이라 한다. 대응각이란 합동인 두 개의 다각형을 포개었을 때 똑같이 겹쳐지는 각을 말한다. 대응각의 크기는 항상 똑같다. 두 개의 삼각형이 있을 때, 세 쌍의 각의 크기가 모두 같으면 두 개의 삼각형은 닮음 혹은 합동이다. (닮음과 합동은 대응변의 길이의 비에 의해 결정된다.) 예를 들어 아래 그림에서 세 쌍의 대응각은 각 ㄱ과 각 ㄹ, 각 ㄴ과 각 ㅂ, 각 ㄴ과 각 ㅁ 이다. 각 ㄱ의 크기가 80°, 각 ㄴ의 크기가 60°, 각 ㅁ의 크기가 40°, 각 ㅂ의 크기가 60°라면 각 ㄱ과 대응각인 각 ㄹ의 크기는 80°, 각 ㅁ과 대응각인 각 ㅁ은 40°이다. 대응각과 대응변을 이용한 합동과 닮음의 조건은 다음과 같다. 1) SSS – SSS합동은 세 쌍의 대응변의 길이가 같을 때 – SSS닮음은 세 쌍의 대응변의 길이의 비가 같을 때 2) SAS – SAS합동은 두 쌍의 대응변의 길이가 같고, 그 끼인각의 크기가 같을 때 – SAS닮음은 두 쌍의 대응변의 길이의 비가 같고 그 끼인 각의 크기가 같을 때 3) ASA(AA) - ASA합동은 한 쌍의 대응변의 길이가 같고, 양 끝각의 크기가 같을 때 - AA닮음은 두 대응각의 크기가 같을 때