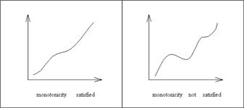
실함수 ƒ(x)에 관해 정의역 내의 임의의 구간 (a,b)에서 a>b일 때 ƒ(a)≥ƒ(b)이고 이 구간 내의 임의의 값 x에 대해 ƒ'(x) > 0 이면 이 함수는 구간 (a,b)에서 단조증가한다고 한다. 어떤 수열이나 함수가 있을 때, 해당 수열이나 함수가 정의된 구간에서 감소하지 않는 경우를 단조증가, 증가하지 않는 경우를 단조감소 함수라고 한다. 위 그림에서 오른쪽 그래프의 경우 중간에 감소하는 구간이 존재하므로 해당 그래프는 단조증가 함수가 아니나, 왼쪽의 그래프의 경우 감소하는 구간이 존재하지 않으므로 단조증가 함수라고 할 수 있다. 결국 감소하는 구간이 없는 경우란 값이 일정하거나 증가하는 구간밖에 없는 경우가 된다. 이 단조증가에서 모든 구간에서 항상 수치가 증가하는 경우를 ‘강한 단조증가’라고 하기도 한다.