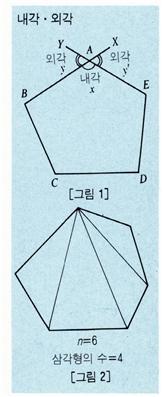
[요약] 꼭짓점을 이루는 두 변의 내부의 각을 내각이라 하고, 한 변의 연장선과 이웃하는 다른 한 변이 이루는 각을 외각이라 한다. 내각과 외각의 크기는 보각(補角)의 관계가 있다. 다각형의 각 꼭짓점(頂點)에서 이웃하는 두변이 이루는 내부의 각을 내각이라 하고, 한 변의 연장선과 이웃하는 다른 한 변이 이루는 각을 외각이라 한다. 따라서 한 꼭짓점에서의 내각과 외각의 크기는 보각(補角) 관계가 있다. 예를 들면 [그림 1]의 다각형 ABC…에서 꼭짓점 A의 내각은 x이며, 외각은 y이고, (∠x의 크기)+(∠y의 크기)=180˚이다. 또 외각 y의 맞꼭지각(對頂角) y’도 외각이 되므로 한 꼭짓점 A에 대한 외각은 두 개가 있으며, 이들은 서로 맞꼭지각이 되므로 그 크기는 같다. 유클리드 기하학에서는 삼각형의 3내각의 크기의 합은 180˚(=2직각)이다. 따라서 삼각형의 한 외각의 크기는 그 두 내대각의 크기의 합과 같다. 이 정리는 평행선의 공리와 정리(定理)에 의해 증명된다. n각형은 한 꼭짓점에서 그을 수 있는 n-3개의 대각선(對角線)에 의해서 n-2개의 삼각형으로 나누어지므로, 그 내각의 크기의 합은 180(n-2)˚이다[그림 2]. 이 관계는 볼록다각형에서나 오목다각형에서나 다같이 성립한다. 그리고 모든 다각형(볼록다각형)의 외각의 합은 360˚이다. 이것은 180n˚([그림 1]에서 ∠x와 ∠y의 크기의 합이 180˚이므로, 그n배)에서 내각의 크기의 합(=180(n-2)˚)을 빼면 360˚가 된다.