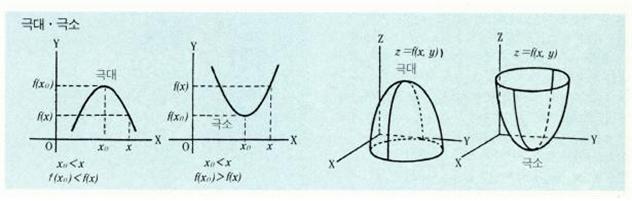
함수 f(x)의 x=x₀에서의 값 f(x₀)이 그 점의 모든 f(x)의 값보다 클(작을) 때 f(X₀)을 극대(극소)라 하고, 이때의 f(x₀)의 값을 극대값(극소값)이라 한다. x가 증가하면서 x₀을 지날 때 f(x)가 증가에서 감소로 변하면 f(x₀)은 극대이고, f(x)가 감소에서 증가로 변하면 f(x₀)은 극소이다. 따라서 극소가 극대보다 클 수도 있다. f(x)가 미분가능이고 그 도함수(導函數) f’(x)의 값이 x=x₀의 전후에서 극대이면 f’(x)의 부호는 +에서 -로 변하고, 극소일 때는 -에서 +로 변한다. 따라서 f’(x)=0이 된다. 이것을 이용하면 극대·극소를 구할 수 있다. 두 변수의 함수 z=f(x, y)는 곡면(曲面)으로 표시할 수 있는데, 그 곡면에서 모자의 꼭대기처럼 된 점이 극대, 사발의 밑바닥처럼 된 점이 극소이다.