증명하고 싶은 명제의 결론이 거짓이라고 가정하였을 때 모순되는 가정이 나온다는 것을 보여주어 결국은 명제가 참이라는 것을 증명하는 방법이다. 예를 들어, 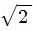가 유리수가 아님을 귀류법으로 증명하는 과정은 다음과 같다. 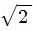가 유리수라고 가정하면  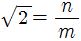(m, n은 정수, 단 m ≠ 0)과 같은 기약분수로 나타낼 수 있다. 이 식에서 2m² = n²이 짝수이므로 n은 짝수이다. 즉, n = 2k인 k(k는 정수)가 있다. 이 두 식에서 m² = 2k²을 얻는다. 역시 m²이 짝수이므로 m도 짝수이다. m, n이 모두 짝수가 된다면 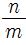이 기약분수가 아니므로 이것은 모순이다. 따라서 가정 '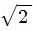는 유리수이다'는 거짓이다. 즉, 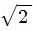는 무리수이다.