거리(distance, 距離)
 2016-10-10
2016-10-10
① N차원 유클리드 공간에서는 두 점 x=(x₁, …, ), y=(y₁, …, ) 사이의 거리는 p(x, y) = 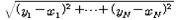 과 같아진다. 이 P(x, y)는 다음 세 가지 성질을 가진다.
㉠ p(x, y)≥0인데 등호는 x=y일 때에 한한다.
㉡ p(x, y)=p(y, x).
㉢ 임의의 3점 x, y, z에 대해 p(x, z)≤p(x, y)+p(y, z). 일반의 위상공간 X에서는 그 임의의 원 x, y에 대해 위의 3가지 성질(이것을 거리의 공리라고함)을 만족시키는 실수 p(x, y)가 일의적으로 대응할때 X에 거리 또는 계량이 정해졌다고 하고, p(x, y)를 두 점 x, y의 거리라고 한다.
선형공간에서는 보통 놈 ∥x-y∥에 의해 거리를 정의한다.
② 리만공간에서는 두 점 (x¹ , x² , …), (x¹+dx¹, x²+dx², …)사이 거리 ds는
과 같아진다. 이 P(x, y)는 다음 세 가지 성질을 가진다.
㉠ p(x, y)≥0인데 등호는 x=y일 때에 한한다.
㉡ p(x, y)=p(y, x).
㉢ 임의의 3점 x, y, z에 대해 p(x, z)≤p(x, y)+p(y, z). 일반의 위상공간 X에서는 그 임의의 원 x, y에 대해 위의 3가지 성질(이것을 거리의 공리라고함)을 만족시키는 실수 p(x, y)가 일의적으로 대응할때 X에 거리 또는 계량이 정해졌다고 하고, p(x, y)를 두 점 x, y의 거리라고 한다.
선형공간에서는 보통 놈 ∥x-y∥에 의해 거리를 정의한다.
② 리만공간에서는 두 점 (x¹ , x² , …), (x¹+dx¹, x²+dx², …)사이 거리 ds는 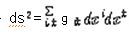 로 정해진다.
g
로 정해진다.
g 는 기본텐서.
③ 추상공간에서의 거리는 일반적으로 정해진 집합의 각 원소를 점으로 생각함으로써 구성되는 추상공간에 대해서는 그 두 원소 x, y에 대해 ㉠ (x, y)≥0 그리고 또 (x, x)=0, ㉡ (x, y)=(y, x), ㉢ (x, z)≤(x, y)+(y, z), ㉣ (x, y)=0이 면 x=y라는 4개의 공준을 만족시키는 실수 (x, y)가 있을 때 이것을 이추상공간에서의 거리라고 정의한다.
그 중에서도 가장 많이 쓰이는 것은 자신의 스칼라곱으로 정의되는 놈
는 기본텐서.
③ 추상공간에서의 거리는 일반적으로 정해진 집합의 각 원소를 점으로 생각함으로써 구성되는 추상공간에 대해서는 그 두 원소 x, y에 대해 ㉠ (x, y)≥0 그리고 또 (x, x)=0, ㉡ (x, y)=(y, x), ㉢ (x, z)≤(x, y)+(y, z), ㉣ (x, y)=0이 면 x=y라는 4개의 공준을 만족시키는 실수 (x, y)가 있을 때 이것을 이추상공간에서의 거리라고 정의한다.
그 중에서도 가장 많이 쓰이는 것은 자신의 스칼라곱으로 정의되는 놈 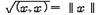 를 써서 (x, y)=∥x-y∥로 표시 하는 것이다.
④ 각거리라고도 한다.
구면 위의 점에 관하여는 구면좌표로 표시한 두 점 사이의 각. 단위 구면을 쓰면 두 점을 지나는 대원의 호의 길이로 표시된다.
를 써서 (x, y)=∥x-y∥로 표시 하는 것이다.
④ 각거리라고도 한다.
구면 위의 점에 관하여는 구면좌표로 표시한 두 점 사이의 각. 단위 구면을 쓰면 두 점을 지나는 대원의 호의 길이로 표시된다.
- 다음
- 거리공간(metric space, 距離空間) 2016.10.10
- 이전
- 구면계 [spherometer, 球面計] 2016.10.10