감마분포(gamma distribution)
 2016-10-04
2016-10-04
변량 X에 관한 분포함수 F(χ)의 미분이
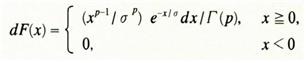 과 같은 분포. 여기서
과 같은 분포. 여기서 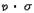 는 상수, Γ(p)는 p의 Γ함수이다. 이것을 또 지수 p의 오일러분포라고도 한다. 모평균은
는 상수, Γ(p)는 p의 Γ함수이다. 이것을 또 지수 p의 오일러분포라고도 한다. 모평균은 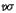 , 모분산은
, 모분산은 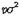 이며 특히 p=1인 경우를 지수분포라고 한다.
이며 특히 p=1인 경우를 지수분포라고 한다. 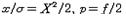 로 두었을 때 X²의 분포를 자유도 f인 X²분포라고 한다. 자유도가 f₁,f₂로서 서로 독자적으로 X²분포를 하는 변량을 더하면 이것은 자유도 (f₁+f₂)인 X²분포를 한다. 원점을 β만큼 이동했을 경우 위치모수(location parameter) β의 피어슨Ⅲ형 분포라고도 한다. 정규분포 N(m, δ²)에서 X²=(x-m)²/δ²으로 두면, 이것은 자유도 1인 X²분포와 같게 된다. 또 프와송분포의 부분합은
로 두었을 때 X²의 분포를 자유도 f인 X²분포라고 한다. 자유도가 f₁,f₂로서 서로 독자적으로 X²분포를 하는 변량을 더하면 이것은 자유도 (f₁+f₂)인 X²분포를 한다. 원점을 β만큼 이동했을 경우 위치모수(location parameter) β의 피어슨Ⅲ형 분포라고도 한다. 정규분포 N(m, δ²)에서 X²=(x-m)²/δ²으로 두면, 이것은 자유도 1인 X²분포와 같게 된다. 또 프와송분포의 부분합은
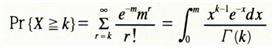 와 같이 Γ분포의 분포함수로써 표시할 수 있다. 자유도(f, ∞)인 F분포에서는 fF가, 자유도(∞, f)인 F분포에서는 fF가, 어느 것이나 자유도 f인 X²분포를 한다.
와 같이 Γ분포의 분포함수로써 표시할 수 있다. 자유도(f, ∞)인 F분포에서는 fF가, 자유도(∞, f)인 F분포에서는 fF가, 어느 것이나 자유도 f인 X²분포를 한다.
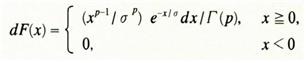 과 같은 분포. 여기서
과 같은 분포. 여기서 - 다음
- 감마함수(gamma function) 2016.10.04
- 이전
- 갈루아 이론(Galois theory) 2016.10.04

관련 콘텐츠





























