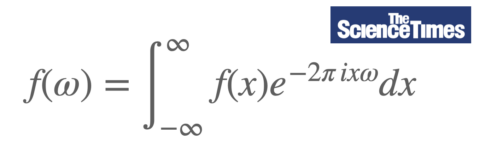고속푸리에변환(fast Fourier transform)
 2016-07-28
2016-07-28
푸리에변환에 근거하여 근사공식을 이용한 이산푸리에변환(discrete transform)을 계산할 때 연산횟수를 줄일 수 있도록 고안된 알고리즘이다.
고속푸리에변환은 1960년대 중반 J.W.콜리와 J.W.터키에 의해 일반적으로 알려지게 되었는데, 그보다 20년쯤 전부터 몇몇 사람들에 의해 독립저그로 발견되어 사용되어 왔다. N개 복소수의 조(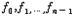 )에서 (
)에서 (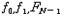 )로의 1차 변환(이산푸리에변환이라고 함) 및 그 역변환을 능률적으로 계산하는 산법이다.
)로의 1차 변환(이산푸리에변환이라고 함) 및 그 역변환을 능률적으로 계산하는 산법이다.
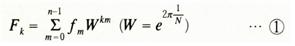 ①을 그대로 계산하면
①을 그대로 계산하면 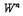 의 계산을 별도로 쳐도 N²회 곱셈을 해야 하는데, 고속푸리에변환에 따르면 약 (N/2)log₂N회의 복소곱셈으로 족하다. 그 원리는 N이 N₁N₂로 인수분해될 때 ①의 계산을
의 계산을 별도로 쳐도 N²회 곱셈을 해야 하는데, 고속푸리에변환에 따르면 약 (N/2)log₂N회의 복소곱셈으로 족하다. 그 원리는 N이 N₁N₂로 인수분해될 때 ①의 계산을
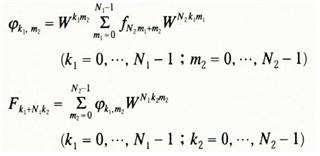 와 같이 낮은 차 변환으로 2단계로 분해 실행할 수 있는 데 있다. 특히 N이 2의 거듭제곱 2ⁿ이면 N=N₁×2 또는 2×N₂의 분해를 되풀이 적용함으로써 최종적으로 곱셈 회수를 N(n-2)/2 정도로 내릴 수 있다. 이 밖에 한쪽 인수를 3,4,5,6.8 등으로 한 여러 가지 변법이 알려져 있다. 고속푸리에변환과 그 역변환에 의해 시계열과 그 주파수스펙트럼 사이의 변환이 자유롭게 되므로 시계열의 상관함수·합성곱의 계산·필터링 등이 주파수스펙트럼을 경유하여 고속으로 계산되고 고속푸리에변환을 위한 전용 마이크로 처리장치도 시판되므로 수치계산에 의한 음성 등의 실시간분석합성·디지틀필터·영상처리 등으로 많이 이용되고 있다.
와 같이 낮은 차 변환으로 2단계로 분해 실행할 수 있는 데 있다. 특히 N이 2의 거듭제곱 2ⁿ이면 N=N₁×2 또는 2×N₂의 분해를 되풀이 적용함으로써 최종적으로 곱셈 회수를 N(n-2)/2 정도로 내릴 수 있다. 이 밖에 한쪽 인수를 3,4,5,6.8 등으로 한 여러 가지 변법이 알려져 있다. 고속푸리에변환과 그 역변환에 의해 시계열과 그 주파수스펙트럼 사이의 변환이 자유롭게 되므로 시계열의 상관함수·합성곱의 계산·필터링 등이 주파수스펙트럼을 경유하여 고속으로 계산되고 고속푸리에변환을 위한 전용 마이크로 처리장치도 시판되므로 수치계산에 의한 음성 등의 실시간분석합성·디지틀필터·영상처리 등으로 많이 이용되고 있다.
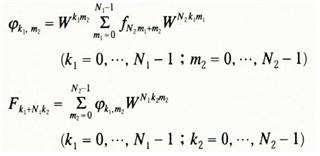 와 같이 낮은 차 변환으로 2단계로 분해 실행할 수 있는 데 있다. 특히 N이 2의 거듭제곱 2ⁿ이면 N=N₁×2 또는 2×N₂의 분해를 되풀이 적용함으로써 최종적으로 곱셈 회수를 N(n-2)/2 정도로 내릴 수 있다. 이 밖에 한쪽 인수를 3,4,5,6.8 등으로 한 여러 가지 변법이 알려져 있다. 고속푸리에변환과 그 역변환에 의해 시계열과 그 주파수스펙트럼 사이의 변환이 자유롭게 되므로 시계열의 상관함수·합성곱의 계산·필터링 등이 주파수스펙트럼을 경유하여 고속으로 계산되고 고속푸리에변환을 위한 전용 마이크로 처리장치도 시판되므로 수치계산에 의한 음성 등의 실시간분석합성·디지틀필터·영상처리 등으로 많이 이용되고 있다.
와 같이 낮은 차 변환으로 2단계로 분해 실행할 수 있는 데 있다. 특히 N이 2의 거듭제곱 2ⁿ이면 N=N₁×2 또는 2×N₂의 분해를 되풀이 적용함으로써 최종적으로 곱셈 회수를 N(n-2)/2 정도로 내릴 수 있다. 이 밖에 한쪽 인수를 3,4,5,6.8 등으로 한 여러 가지 변법이 알려져 있다. 고속푸리에변환과 그 역변환에 의해 시계열과 그 주파수스펙트럼 사이의 변환이 자유롭게 되므로 시계열의 상관함수·합성곱의 계산·필터링 등이 주파수스펙트럼을 경유하여 고속으로 계산되고 고속푸리에변환을 위한 전용 마이크로 처리장치도 시판되므로 수치계산에 의한 음성 등의 실시간분석합성·디지틀필터·영상처리 등으로 많이 이용되고 있다.- 다음
- 고유방정식(proper equation, 固有方程式) 2016.07.28
- 이전
- 고립점(isolated point, 孤立點) 2016.07.28