고계미분계수(differenial coefficient of higher order, 高階微分係數)
 2016-07-28
2016-07-28
함수 ƒ(x)에서 x의 변화량을 Δx라고 할 때, Δx에 대한 ƒ(x)의 변화량 ƒ(x+Δx) - ƒ(x)의 비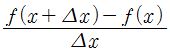 에 x가 0으로 가는 극한을 취하면
에 x가 0으로 가는 극한을 취하면 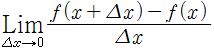 가 된다. 이를 도함수라 하며 ƒ'(x)로 표현한다. 그런데 도함수에 대해서 또 미분을 할 수 있다. 이때는
가 된다. 이를 도함수라 하며 ƒ'(x)로 표현한다. 그런데 도함수에 대해서 또 미분을 할 수 있다. 이때는 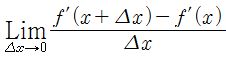 가 된다. 이를 2계도함수라 한다. 마찬가지로 낮은 계수의 도함수에 대해서 미분을 해서 높은 계수의 도함수를 얻어낼 수 있는데, 2계도함수 이상의 도함수들을 고계도함수라 한다. 미분계수란 도함수에 특정한 값을 대입해 얻어낸 계수를 말한다. 즉, ƒ'(a)이다. 마찬가지로 고계미분계수란 고계도함수에 특정한 값을 대입해 얻어낸 값이다.
가 된다. 이를 2계도함수라 한다. 마찬가지로 낮은 계수의 도함수에 대해서 미분을 해서 높은 계수의 도함수를 얻어낼 수 있는데, 2계도함수 이상의 도함수들을 고계도함수라 한다. 미분계수란 도함수에 특정한 값을 대입해 얻어낸 계수를 말한다. 즉, ƒ'(a)이다. 마찬가지로 고계미분계수란 고계도함수에 특정한 값을 대입해 얻어낸 값이다.
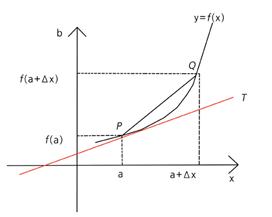
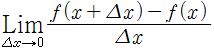 가 된다. 이를 도함수라 하며 ƒ'(x)로 표현한다. 그런데 도함수에 대해서 또 미분을 할 수 있다. 이때는
가 된다. 이를 도함수라 하며 ƒ'(x)로 표현한다. 그런데 도함수에 대해서 또 미분을 할 수 있다. 이때는 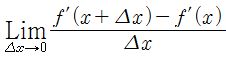 가 된다. 이를 2계도함수라 한다. 마찬가지로 낮은 계수의 도함수에 대해서 미분을 해서 높은 계수의 도함수를 얻어낼 수 있는데, 2계도함수 이상의 도함수들을 고계도함수라 한다. 미분계수란 도함수에 특정한 값을 대입해 얻어낸 계수를 말한다. 즉, ƒ'(a)이다. 마찬가지로 고계미분계수란 고계도함수에 특정한 값을 대입해 얻어낸 값이다.
가 된다. 이를 2계도함수라 한다. 마찬가지로 낮은 계수의 도함수에 대해서 미분을 해서 높은 계수의 도함수를 얻어낼 수 있는데, 2계도함수 이상의 도함수들을 고계도함수라 한다. 미분계수란 도함수에 특정한 값을 대입해 얻어낸 계수를 말한다. 즉, ƒ'(a)이다. 마찬가지로 고계미분계수란 고계도함수에 특정한 값을 대입해 얻어낸 값이다.

- 다음
- 고립점(isolated point, 孤立點) 2016.07.28
- 이전
- 고계도함수(higher order derivatives, 高階導函數) 2016.07.28






























