미분방정식의 일반해는 임의의 상수나 또는 임의의 함수를 포함하므로 정해진 영역이나 구간의 경계에서 해를 만족시킬 적당한 조건을 정해서 특수해를 구하는 문제를 경계값문제라고 한다. 이때의 조건을 경계조건이라고 한다. 보통은 공간변수의 영역 또는 구간의 경우에 한정하며 시간변수의 초기값을 초기값문제, 초기조건이라고 한다. 단 공간변수의 구간 [a,b]에서 정의된 상미분방정식에 대해서도 a의 조건을 초기조건, b의 조건을 종기조건이라고 한다. 경계조건과 초기조건이 결합된 경우도 있다. 자연현상에 관한 한 이들의 조건이 저절로 정해지는 경우가 많다. 2계 편미분방정식에서 해를 u, 경계의 법선 방향의 미분연산자를 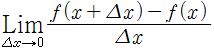, 또 α, β를 상수로 하여 경계 위에서 각기 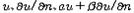, n의 조건을 다루는 경계값문제, 경계조건을 각기 제1종(디리클레), 제2종(노이만), 제3종 경계값문제, 경계조건이라고 한다. 경계 위에서 0의 조건으로 하는 경우가 많다.