[요약] 유리수를 계수로 갖는 대수적방정식이 주어졌을 때, 이 방정식의 근이 되는 복소수를 말한다. 대수적 수는 실수, 복소수 모두 존재하나 대수적 수가 아닌 실수도 존재한다. 유리수를 계수로 하는 n차(n > 0) 대수방정식 ∫(x)＝a₀xⁿ＋a₁x^n-1＋a₂x^n-2＋…＋a_n＝0의 근 α. 특히 f(x)가 기약이면 α는 n차의 대수적수라 하고 원래의 방정식 f(x)＝0을 α의 정의방정식(定義方程式)이라고 한다. 예를 들면, 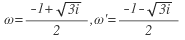는 방정식 x²＋x＋1＝0의 근이므로 대수적 수이고, x²＋x＋1은 2차 기약다항식이기 때문에 ω, ω’는 2차의 대수적수이다. 또 x²＋x＋1은 이들의 정의방정식이다. 물론 유리수 자신도 대수적수이다. 대수적수의 전체 A는 유리수체 R의 확대체이고 대수적으로 닫힌 체이다. 특히 최고차항의 계수가 1인 정의방정식의 근이 되는 수를 대수적 정수라고 한다. 대부분의 대수적 수는 부진근수(不盡根數)로 표시할 수 있다. 그러나 거듭제곱근을 사용해서 나타낼 수 없는 대수적 수도 존재한다. 왜냐하면 4차보다 고차인 대수방정식은 일반적으로 거듭제곱근을 사용해서 풀 수 없기 때문이다. 거듭제곱근을 사용하여 나타낼 수 있는 대수적 수는 특히 중요한데, 이들은 자와 컴퍼스만으로 평면 위에 작도할 수 있기 때문이다. 반대로 자와 컴퍼스를 사용해서 작도할 수 있는 선분은 모두 제곱근만 들어 있는 부진근수로 나타낼 수 있다. 대수적 수는 다음과 같이 분류된다.