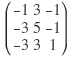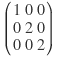[요약] ‘대각 행렬로 만들 수 있는’ 이라는 뜻이다. 행렬에서 쓰이는 개념으로, 말 그대로 ‘대각 행렬로 만들 수 있는’ 이라는 뜻이다. 예를 들어 아래의 행렬을 보자.

 

이는 대각행렬과는 전혀 관련 없어 보이지만 위의 행렬은 행간 연산을 통해 다음과 같은 대각행렬로 만들 수 있다.

 

이는 곧 위 행렬의 Eigen value와 같다. 즉, 만일 n*n행렬 F가 n개의 eigenvalue를 가진다면 이때의 행렬 F는 대각화 가능하다. 대각화 가능하다는 성질은 해당 행렬이 사용된 연립방정식을 푸는 데 매우 유용하다. 예를 들어 위의 경우,

－x－3y－z＝0 －3x＋5y－z＝0 －3x＋3y＋z＝0

이라는 연립방정식을 풀기 위해 대각화 가능함의 성질을 이용하면 쉽게 x, y, z의 값을 찾을 수 있는 것이다.