다항정리[multinomial theorem, 多項定理]
 2015-12-18
2015-12-18
[요약] 3항 이상의 다항식의 거듭제곱을 전개할 때, 변수의 차수와 계수항을 이용하는 정리이다. 2항 다항식의 전개는 이항정리라고 한다.
m, n이 양의 정수이고 a1, a2, …, am가 임의의 수(실수 또는 복소수) 또는 단항식일 때, 다항식 a1+a2+…+am의 n 거듭제곱은 다음과 같이 전개할 수 있다.
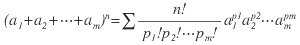 이것을 다항정리라 한다. 여기서 p1, p2, …, pm은 0 또는 자연수이며 ∑는 p1+p2+…+pm=n을 만족시키는 모든 p1, p2, …, pm에 대하여 더한 합을 의미한다. 그리고
이것을 다항정리라 한다. 여기서 p1, p2, …, pm은 0 또는 자연수이며 ∑는 p1+p2+…+pm=n을 만족시키는 모든 p1, p2, …, pm에 대하여 더한 합을 의미한다. 그리고 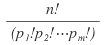 을 다항계수라 하는데 이것은 서로 다른 n개의 공을 개, p1개, p2개…, pm개로 총 m개의 묶음으로 나눌 경우의 수와 같다. 특히 일 m=3일때, 즉 항이 세 개일 때의 다항정리는 다음과 같으며 이를 이항정리라고 한다.
을 다항계수라 하는데 이것은 서로 다른 n개의 공을 개, p1개, p2개…, pm개로 총 m개의 묶음으로 나눌 경우의 수와 같다. 특히 일 m=3일때, 즉 항이 세 개일 때의 다항정리는 다음과 같으며 이를 이항정리라고 한다.
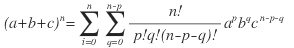
- 다음
- 다항함수[polynomial function] 2015.12.18
- 이전
- 다항식환[polynomial ring, 多項式環] 2015.12.18






























