[요약] 리만적분의 존재에 관련된 사항을 엄밀한 해석적 방법으로 확립하기 위한 정리로 다르부에 의해서 증명되었다. 리만적분의 존재와 관련한 내용을 해석학적(解釋學的) 방법으로 확립하기 위한 정리로 프랑스의 수학자 다르부에 의해 증명되었다. 구간 a ≤ x ≤ b를 의 a＝x₀ < x₁ < … < x_n-1 < x_n＝b의부분구간으로 분할하고 이 구간에서 정의된 유계(有界)의 함수를 f(x), 어떤 상수 m, M에 대하여 m ≤ f(x) ≤ (a ≤ x ≤ b)라 한다. x_i-1 ≤ x ≤ x_i에 대하여 f(x)의 상한(上限)을 M_i, 하한(下限)을 m_i라 할 때, M_i－m_i를 구간 x_i-1 ≤ x ≤ x_i에서의 진폭이라 한다. 각 부분구간의 길이는 δ_i＝x_i－x_i-1이고, 부분구간을 한없이 나누어 n을 무한대(∞)로 놓으면 δ(D)＝maxδ_i는 한없이 0에 가까워지고, 다음 2개의 합, 즉, 다르부의 합 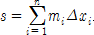, 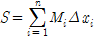는 각각 극한값을 가진다. 이것은 극한의 기법 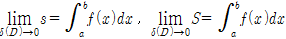로 표시된다.