[요약] 근의 공식이란 a, b, c는 실수이고 a가 0이 아닐 때 이차방정식에서 ax² + bx + c = 0의 해를 구하는 공식이다. 근의 공식이란 a, b, c는 실수이고 a가 0이 아닐 때 이차방정식에서 ax² + bx + c = 0의 해를 구하는 공식이다. 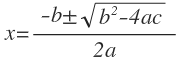(단, b² - 4ac > 0 이다.) * 일차항의 계수(b)가 짝수인 경우에는 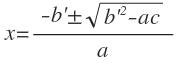(단, b² - ac ≥ 0이다.) 예를 들어 2x² - 2x + 1 = 0의 이차방정식을 근의 공식을 이용하여 해를 구해 보면 x = -(-2)±√((-2)²-2X1 / 2 = 2±√2/2 이다. ※참고 : D = b² - 4ac를 이차방정식의 판별식이라고 한다. 판별식의 값에 따라 방정식의 해가 세 가지로 나뉘게 된다. 1) D > 0일 때 서로 다른 두 실근을 갖는다. 2) D = 0일 때 한 개의 중복되는 실근을 갖는다. (중근) 3) D < 0일 때 서로 다른 허근을 갖는다. (실수범위 내에서 해가 존재하지 않는다.)