[요약] 함수 f(x)가 미분가능하고, f'(x)가 연속일 때, 함수 f(x)의 근삿값을 구하는 식이다. 함수 f(x)가 미분 가능하고, f'(x)가 연속이면, x가 a에 가까운 값이다. 이를테면 x = a + 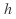h일 때의 함수 f(x)의 값은, 식 f(x) ≒ f(a) + f'(a)(x - a)에 의하여 근사적으로 구할 수 있다. 이 식이 함수 f(x)의 근사식이다. 예를 들면 h > 0이 1에 비하여 충분히 작을 때, (1 + h)ⁿ의 근사식은 (1 + h)ⁿ ≒ 1 + nh이다.