공변벡터[covariant vector]
 2015-11-18
2015-11-18
[요약] 공간벡터 a에 대하여 정의된 실수값을 취하는 함수 Φ(a)가 선형조건(線形條件) Φ(a+b) = Φ(a)+Φ(b), Φ(αa) = αΦ(a) (여기서 a,b는 임의의 벡터, α는 임의의 실수)를 만족할 때 Φ를 공변벡터라 한다.
공간벡터 a에 대해 정의된 실수값을 취하는 함수 Φ(a)가 선형조건(線形條件) Φ(a+b) =Φ(a)+Φ(b), Φ(αa) = αΦ(a)(여기서 a, b는 임의의 벡터, α는 임의의 실수)를 만족시킬 때 를 공변벡터 또는 1차형식이라 한다.
3차원 유클리드 공간 K(서로 직각인 단위벡터를 e1, e2, e3라 한다)에 대해 Φ1 = Φ(e1), Φ2 = Φ(e2), Φ3 = Φ(e3)를 K에 관한 Φ의 성분이라고 한다. 공간 K의 1점 P의 위치좌표를 (x1, x2, x3)라 하고 좌표계(座標系)가 K에서 K’로 옮길 때의 좌표가 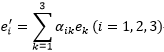 인 관계를 가지고 (e1´, e2´, e3´)로 변환한다고 하면 이 때 Φ의 성분은
인 관계를 가지고 (e1´, e2´, e3´)로 변환한다고 하면 이 때 Φ의 성분은 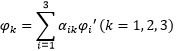 의 관계를 가지고 (e1, e2, e3)에서 (e1´, e2´, e3´)로 변환된다.
의 관계를 가지고 (e1, e2, e3)에서 (e1´, e2´, e3´)로 변환된다.
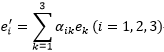 인 관계를 가지고 (e1´, e2´, e3´)로 변환한다고 하면 이 때 Φ의 성분은
인 관계를 가지고 (e1´, e2´, e3´)로 변환한다고 하면 이 때 Φ의 성분은 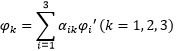 의 관계를 가지고 (e1, e2, e3)에서 (e1´, e2´, e3´)로 변환된다.
의 관계를 가지고 (e1, e2, e3)에서 (e1´, e2´, e3´)로 변환된다.- 다음
- 공비[common ratio, 公比] 2015.11.18
- 이전
- 공변미분[covariant differentiation, 共變微分] 2015.11.18






























