고계도함수[higher order derivatives, 高階導函數]
 2015-11-17
2015-11-17
[요약] n>1일 때, f(n)(x)가 존재하고, f(n)(x)가 연속일 때 f(n)(x)를 f(x)의 고계도함수라고 한다.
고계도함수란 함수를 여러 번 미분한 것을 말한다. 즉, 함수 f가 미분 가능하면 도함수 f´는 또 다른 함수가 된다. 이때, 도함수 f´가 미분 가능한 함수이면 f´의 도함수를 f의 2계도함수라 하고, 2계도함수 f´´가 미분 가능한 함수이면 f´´의 도함수를 f의 3계도함수라 한다. 2계 이상의 도함수를 통틀어서 고계도함수라고 한다.
고계도함수는 일반적으로 가속도를 예로 들 수가 있다. 시간을 미분하면 속도가 되고, 속도를 미분하면 가속도가 된다. 따라서 시간을 2번 미분하면 가속도가 되는 것이다. 이때, 극댓값과 극솟값을 구하고 곡선의 오목과 볼록을 판명해서 곡선을 그려야 한다.
이계도함수의 기호: 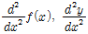 삼계도함수의 기호:
삼계도함수의 기호: 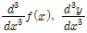 고계도함수(n계도함수)의 기호:
고계도함수(n계도함수)의 기호: 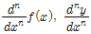




- 다음
- 고계미분계수[differenial coefficient of higher order, 高階微分係數] 2015.11.17
- 이전
- 고계[higher order, 高階] 2015.11.17






























