[요약] x를 거듭제곱하여 a가 될 때 x를 a의 거듭제곱근이라 한다. 일반적으로 n이 자연수일 때 n제곱하여 a가 되는 수 x를 a의 n제곱근이라고 하고, a의 n제곱근은 복소수 범위에서 n개가 있다. 실수(또는 복소수) x를 거듭제곱하여 a가 될 때, x를 a의 거듭제곱근이라 한다. 누승근(累乘根) 또는 멱근(冪根)이라고도 한다. 일반적으로 n이 자연수일 때, xn = a가 되는 수 x, 즉 n제곱하여 a가 되는 수 x를 a의 제곱근이라고 한다. 0의 n제곱근은 0이다. n=2일 때에는 제곱근, n=3일 때는 세제곱근이라 한다. a의 n제곱근은 복소수 범위에서 n개 있다. 그러나 a의 n제곱근중 실수인 것만을 생각하기로 한다면, a<0인 경우, n이 짝수일 때는 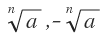의 2개가 있고, 홀수일 때는 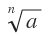하나만 있다. a<0인 경우, n이 짝수일 때는 음수 a의 n제곱근 중 실수인 것은 없고, n이 홀수이면 도 음수로서 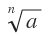하나가 있다.